補数

補数（ほすう、（英: complement）または余数（よすう）とは、ある数 x との和が基準となる数 C に等しくなるような数である。すなわち、補数を x_c とすればこれは x x_c = C を満たす。

C を b 進法の基数の冪 bⁿ とすればこれは、b 進法で bⁿ = 100…00_b と表せる。従ってこの場合、非負の整数 x に対する補数 x_c は x に足して n 1 桁になる最小の整数と言える。

補数は計算機において、減算や負の数を表すためにしばしば利用される。

定義

x を b 進法で n 桁の非負の整数とする。 x に対する基数の補数（英: radix complement）は以下のように定義される：

${\displaystyle b^{n}-x}$

基数が文脈から明らかなら、単に b の補数（英: b's complement）と呼ばれる（例えば二進法における基数の補数は2の補数と呼ばれる）。 同様に、x に対する減基数の補数（英: diminished radix complement）は以下のように定義される：

${\displaystyle (b^{n}-1)-x}$

基数が文脈から明らかなら、単に (b − 1) の補数（英: (b − 1)s' complement）と呼ばれる（例えば二進法における減基数の補数は1の補数と呼ばれる）。

呼称

日本語において、文脈から基数が明らかでない状況で「N の補数」と言った場合、「N 1 進法における減基数の補数」と「N 進法における基数の補数」のどちらを指すか曖昧である。例えば、「9の補数」は「9進法における基数の補数」と「10進法における減基数の補数」のいずれの意味でも用いられ得る。曖昧さを取り除くためには、「基数の補数」か「減基数の補数」のいずれであるかを示したり、基数が何であるかを示す必要がある。

英語において文章上は、例えば基数の補数を nine's complementと書き、減基数の補数を nines' complementと書くことで区別できる。

補数の利用・応用

繰り上がり（繰り下がり）のある計算

補数は身近なところでも利用される。ほぼ無意識のうちに使っているが、繰り上がりのある足し算で使われる 。 例えば、「8 7 = 15] という計算を考える。まず、7 に何を足せば 10 を作れるかを考えると 3 である。8 を 5 3 に分解して、3 7 で 10 を作り、1 の位は残った 5 であるから、合わせて 15 となる。 つまり、1の位の計算で、7 を足す代わりに 7 の補数である 3 を引くことで、繰り上がりのある計算ができる。 これをきちんと数式で書くと

${\displaystyle {\begin{aligned}x y&=x y b^{1}-b^{1}\\&=b^{1} x-(b^{1}-y)\\\end{aligned}}}$

である。 式の最右辺において、${\displaystyle b^{1}}$ は上の位への繰り上がりである。 残りの ${\displaystyle x-(b^{1}-y)}$ が、${\displaystyle y}$ を足す代わりに、${\displaystyle y}$ の補数を引くことを意味する。

この計算方法は、そろばんでも同様に使われる。 つまり 7 を足すときに、繰り上がりが発生するときは、一の珠を 3つ下げる。ほかの数字でも同様。 なお、そろばんでは五珠もあるので、10 の補数のほか、5 の補数も使わなければならない。

繰り下がりのある引き算でも同様である。

補数を利用した減算

補数を利用すると、正整数の減算を加算処理で行うことができる。

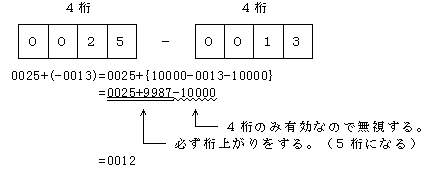
以下に、10 進 5 桁の減算 ${\displaystyle 52934-38917=14017}$ を、補数を用いて加算処理に置き換えた例を説明する。被減数を x、減数を y とし、減算結果を ${\displaystyle x-y\equiv z}$ とする。

• 減数 y の減基数の補数を求める。この計算は、各桁について補数を求めればよいので桁借りが発生せず、簡単に行うことができる。

• 減数 y の基数の補数を求める。これは減基数の補数 ${\displaystyle y'}$ に 1 を加えるだけである。

• 被減数 x と 減数 y の基数の補数とを足し合わせる。このとき、最上桁の桁上がりは無視する（つまり結果から ${\displaystyle 10^{5}}$ を減ずる）。

このように、本来桁借りを考慮しなければならないような減算であっても、補数の概念を利用すれば加算処理に置き換えて計算することができる。

上に挙げたのは10進法の例であるが、これは任意の基数において成り立つ。

この性質により、負整数の表記法として基数の補数を採用すると、最上位桁からの桁上がり（桁あふれ・算術オーバーフロー）を無視すれば、通常の加算処理で負整数の加算（つまり正整数の減算）が行えることになる。この利点のため、2の補数は多くのコンピュータで負整数の内部表現に採用されている。

脚注

注釈

出典

参考文献

• 日本規格協会、情報処理学会 編『JIS X 0005:2002 情報処理用語（データの表現）』日本規格協会、2002年8月31日。 
• ISO; IEC, eds (2015-05). ISO/IEC 2382:2015 Information technology — Vocabulary. ISO/IEC 
• Knuth, Donald E. (1997). The Art of Computer Programming Volume 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley. ISBN 0-201-89684-2 

関連項目

• 加算器
• 2の補数
• 1の補数
• 符号付数値表現